And Why You Should Implement It In Your Organisation
Designing a system is challenging, especially when it involves multiple, sometimes conflicting, disciplines. Complex systems can’t be boiled down to a single, easily solvable function. Design variables from different disciplines often clash like a tangled spider web, making it impossible to comprehend and optimize through intuition. This is where Multidisciplinary Design Optimization (MDO) comes in, automatically finding the best trade-offs without bias or ambiguity.
In this article, we’ll explore how MDO works and why it’s still not a common practice in complex system development.
Simultaneous vs Sequential Optimization
MDO is a design methodology that optimizes a complex system by considering multiple disciplines simultaneously. In the industry, design teams typically work within their specific disciplines or subsystems, optimizing their respective components locally before handing the design off to the next team. This sequential optimization approach is mathematically bound to result in suboptimal designs.
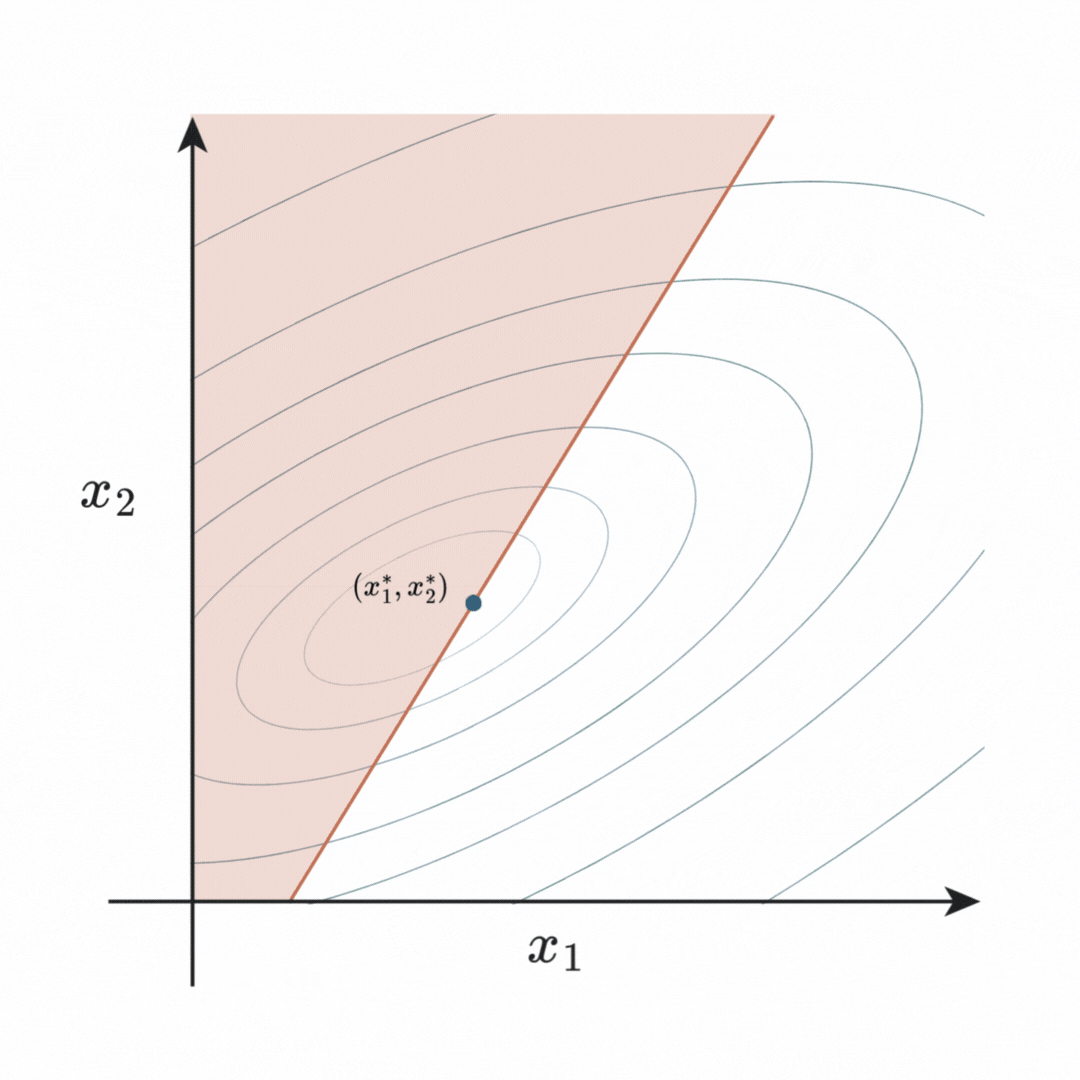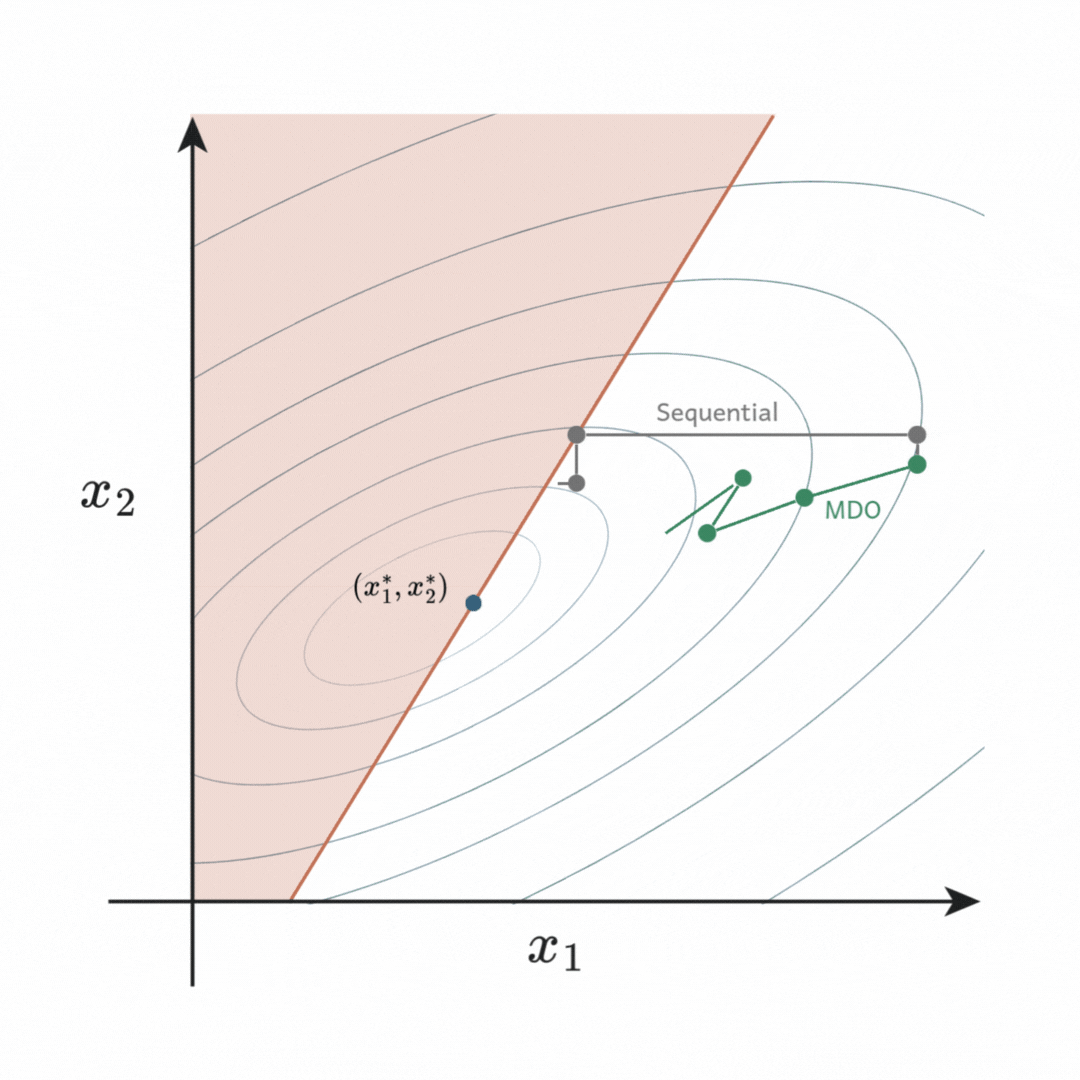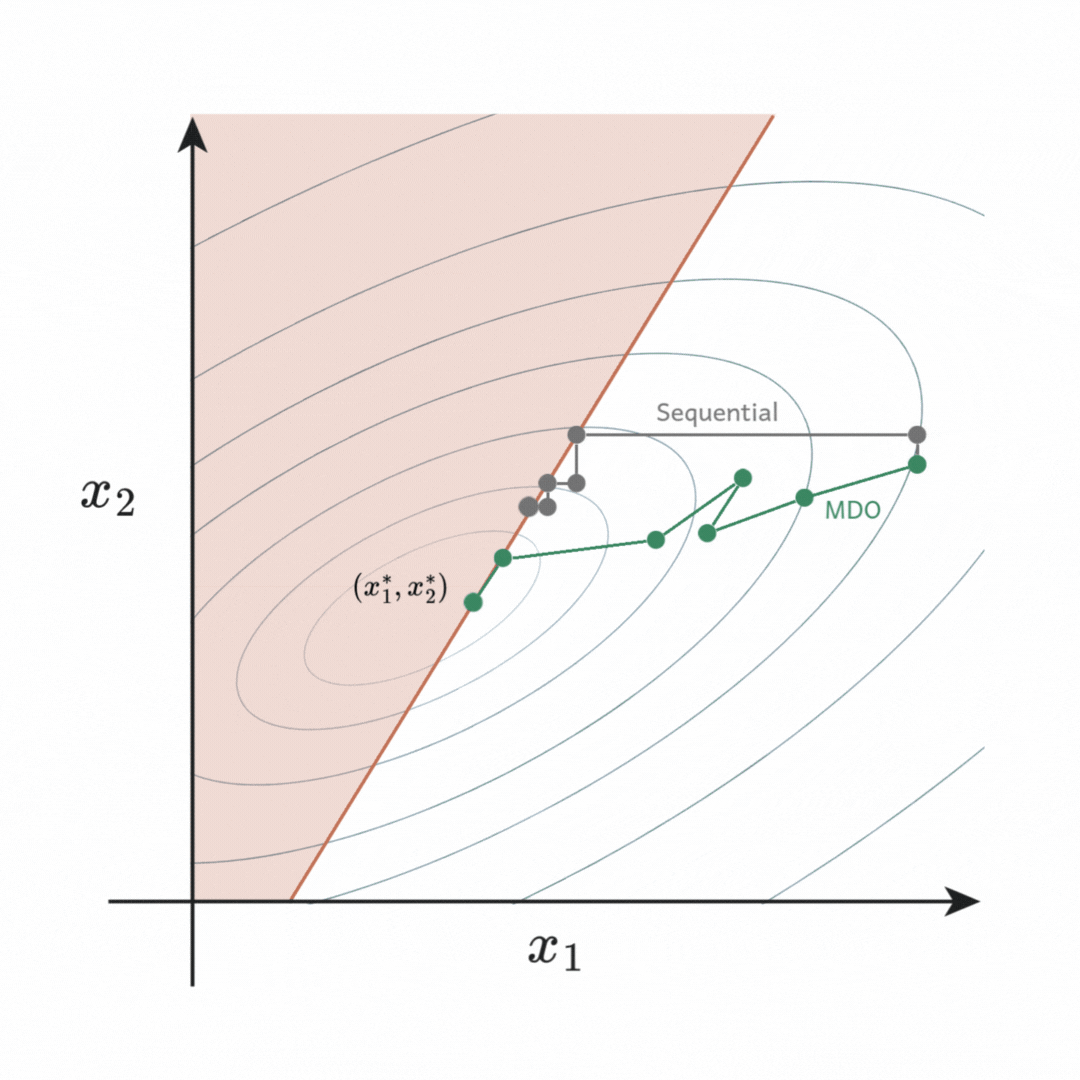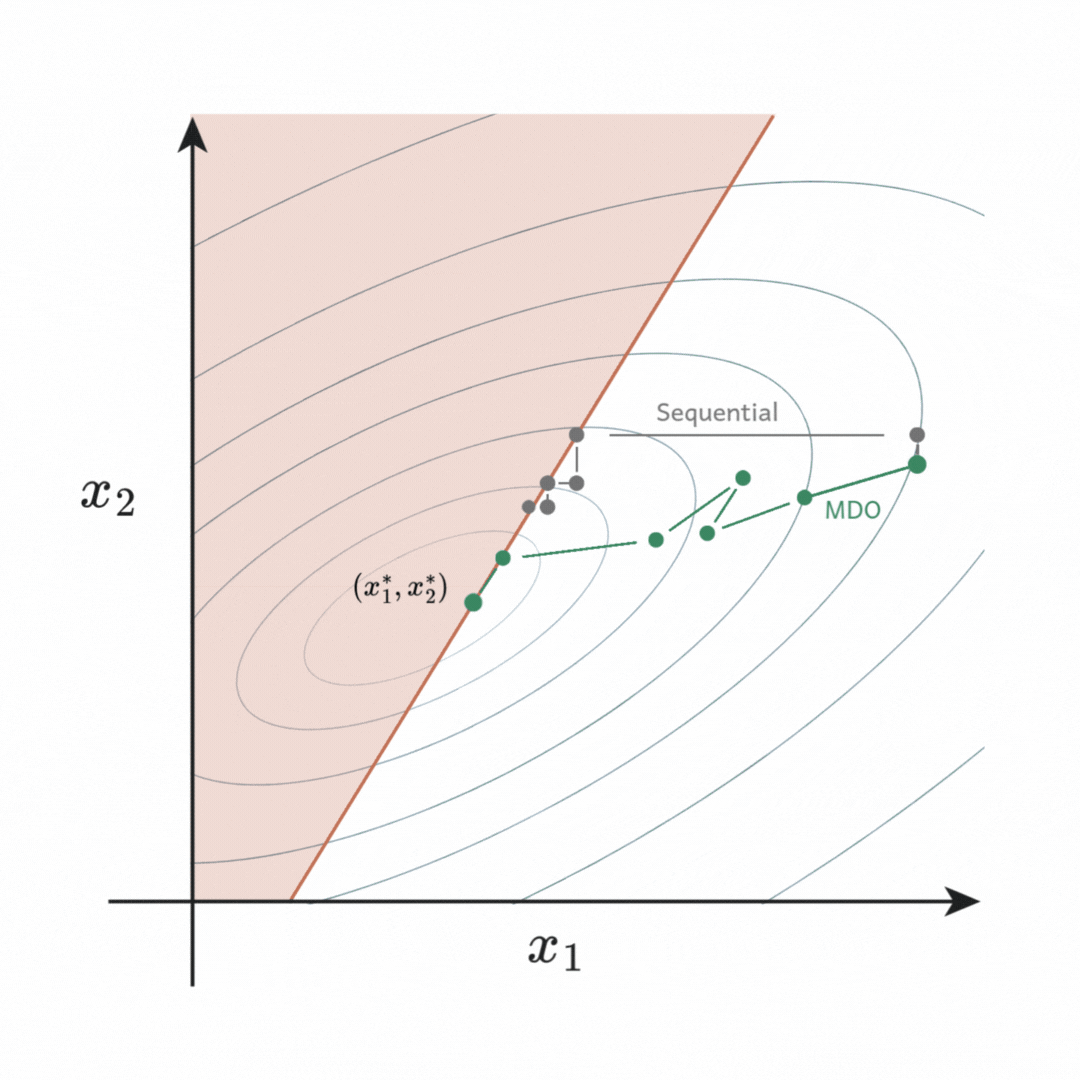
Consider a scenario involving two disciplines, ![]() and
and ![]() , with contours representing an objective function. The optimal values
, with contours representing an objective function. The optimal values ![]() are closest to the centre of the contour while satisfying an arbitrary constraint (red region). In sequential optimization, either
are closest to the centre of the contour while satisfying an arbitrary constraint (red region). In sequential optimization, either ![]() or
or ![]() is adjusted at each step, resulting in a suboptimal design as it fails to find a feasible descent direction upon the constraint. On the other hand, simultaneous optimization allows both variables to be adjusted together, thus a descent direction that leads to the true optimum can be found.
is adjusted at each step, resulting in a suboptimal design as it fails to find a feasible descent direction upon the constraint. On the other hand, simultaneous optimization allows both variables to be adjusted together, thus a descent direction that leads to the true optimum can be found.
In short, MDO produces superior designs compared to the sequential optimization commonly used in engineering organisations today.
A Classic Example: Aerostructural Optimization
Imagine designing the wing shape of an aircraft by varying its wingspan, ![]() , and chord,
, and chord, ![]() , to minimise the required power,
, to minimise the required power, ![]() , for level flight, with a constraint on the bending stress at the root of the wing,
, for level flight, with a constraint on the bending stress at the root of the wing, ![]() .
.
The optimization problem can be formulated as follows:
![Rendered by QuickLaTeX.com \[\begin{aligned} \text{min.} & \quad P(b,\ c) = \frac{Dv}{\eta} \\\ \text{where} &\quad \ D, \ v, \ \eta \ \text{ are drag, velocity and propulsive efficiency} \\\ \text{w.r.t.} & \quad b, \ c \\\ \text{subject to} & \quad 2.5 \sigma_{\text{max}} -\frac{\sigma_{\text{yield}}}{1.5} \leq 0 \end{aligned}\]](https://optimise.systems/wp-content/ql-cache/quicklatex.com-56ffed17501ff716bfc5a2c41bf05c4c_l3.png)
The required power, ![]() , is a function of the wing shape,
, is a function of the wing shape, ![]() and
and ![]() , as it directly affects the drag,
, as it directly affects the drag, ![]() , and drag is related to the lift,
, and drag is related to the lift, ![]() , generated from the wing. The aerodynamics and structural disciplines of the aircraft are coupled, in the way that as the lift increases, the wing will deflect more, but as the deflection angle,
, generated from the wing. The aerodynamics and structural disciplines of the aircraft are coupled, in the way that as the lift increases, the wing will deflect more, but as the deflection angle, ![]() , increases, the lift generated will also reduce**. In such case, numerical methods are needed to converge on feasible solutions for
, increases, the lift generated will also reduce**. In such case, numerical methods are needed to converge on feasible solutions for ![]() and
and ![]() before we can calculate the required power,
before we can calculate the required power, ![]() . This step is known as Multidisciplinary Design Analysis (MDA).
. This step is known as Multidisciplinary Design Analysis (MDA).
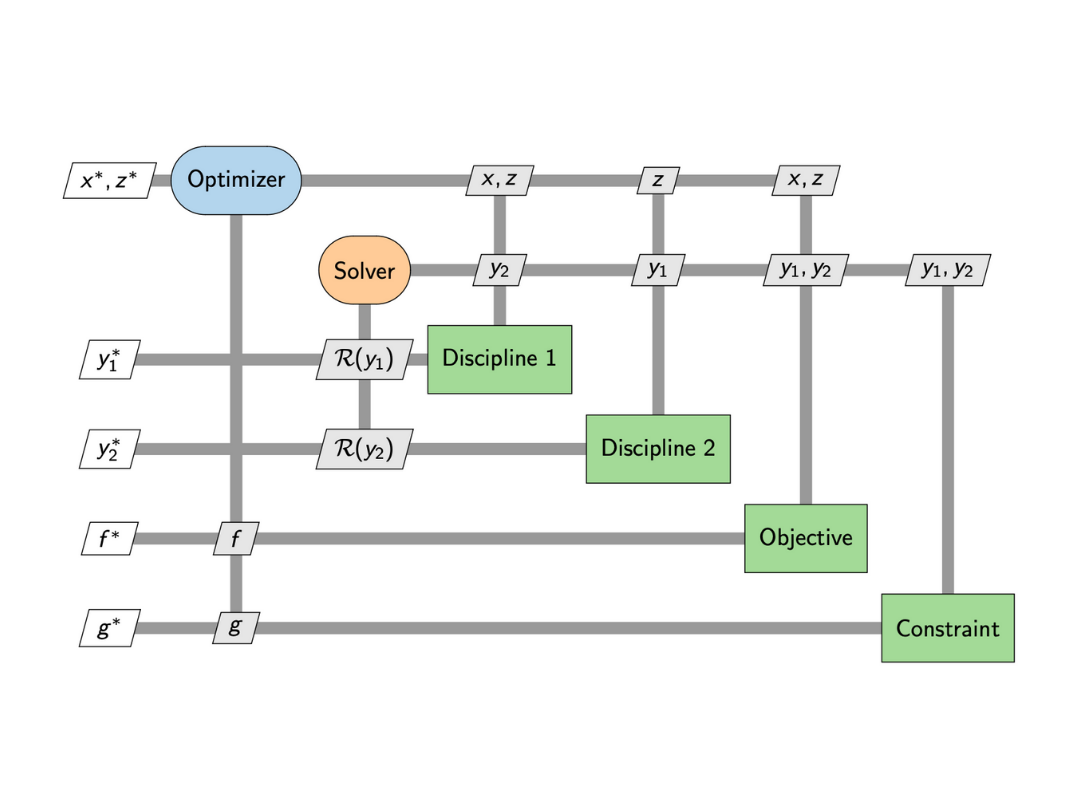
We can use an eXtended Design Structure Matrix (XDSM) diagram to visualise the dependencies between the two disciplines and the execution sequence of the optimization. Initial values of the wing shape design, ![]() and
and ![]() , are inputted to the solvers to determine lift,
, are inputted to the solvers to determine lift, ![]() , and wing deflection,
, and wing deflection, ![]() , which are used to compute drag,
, which are used to compute drag, ![]() . These intermediate state variables are then used to compute the required power, P, and check against the stress constraint
. These intermediate state variables are then used to compute the required power, P, and check against the stress constraint ![]() .
.
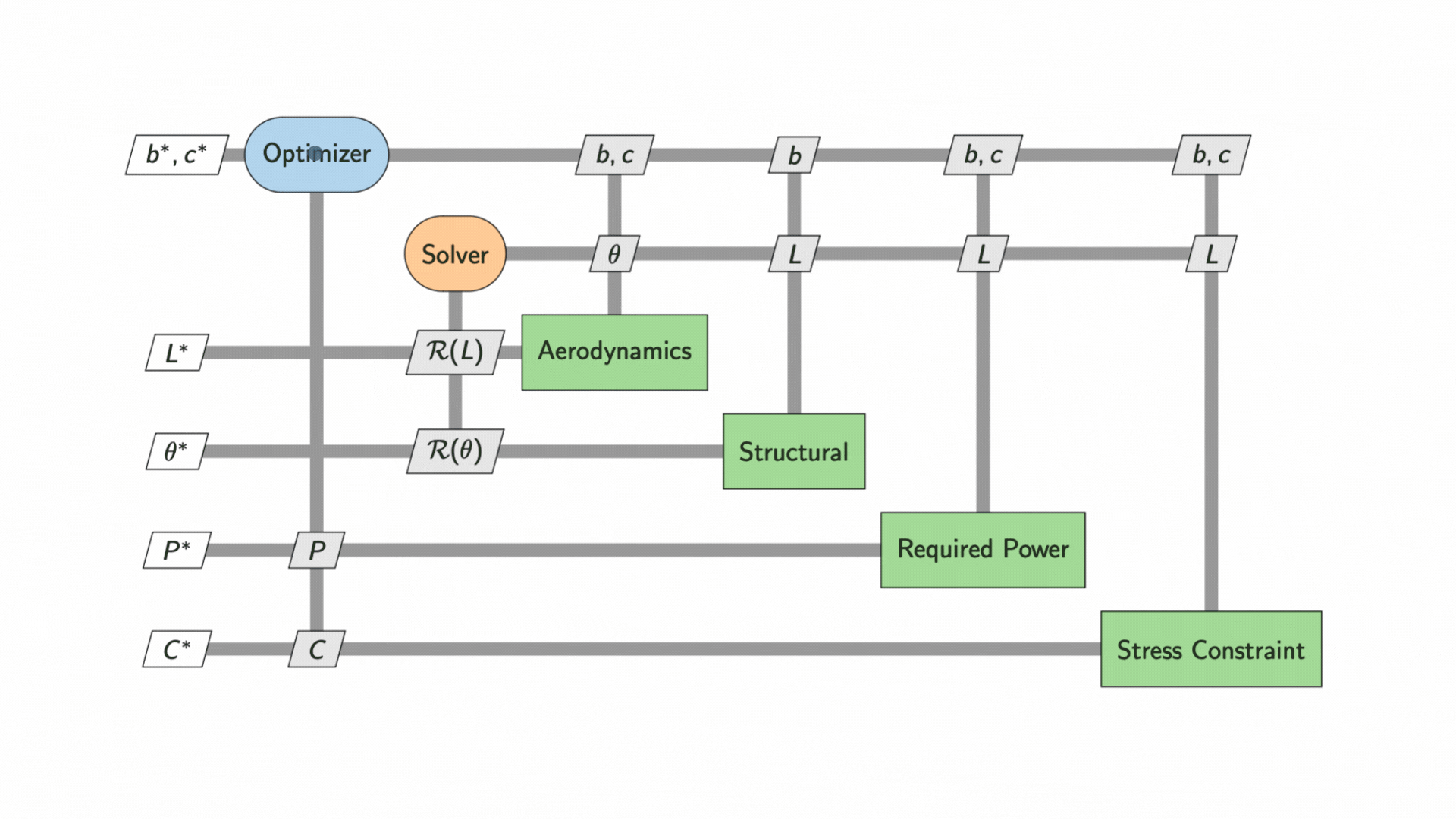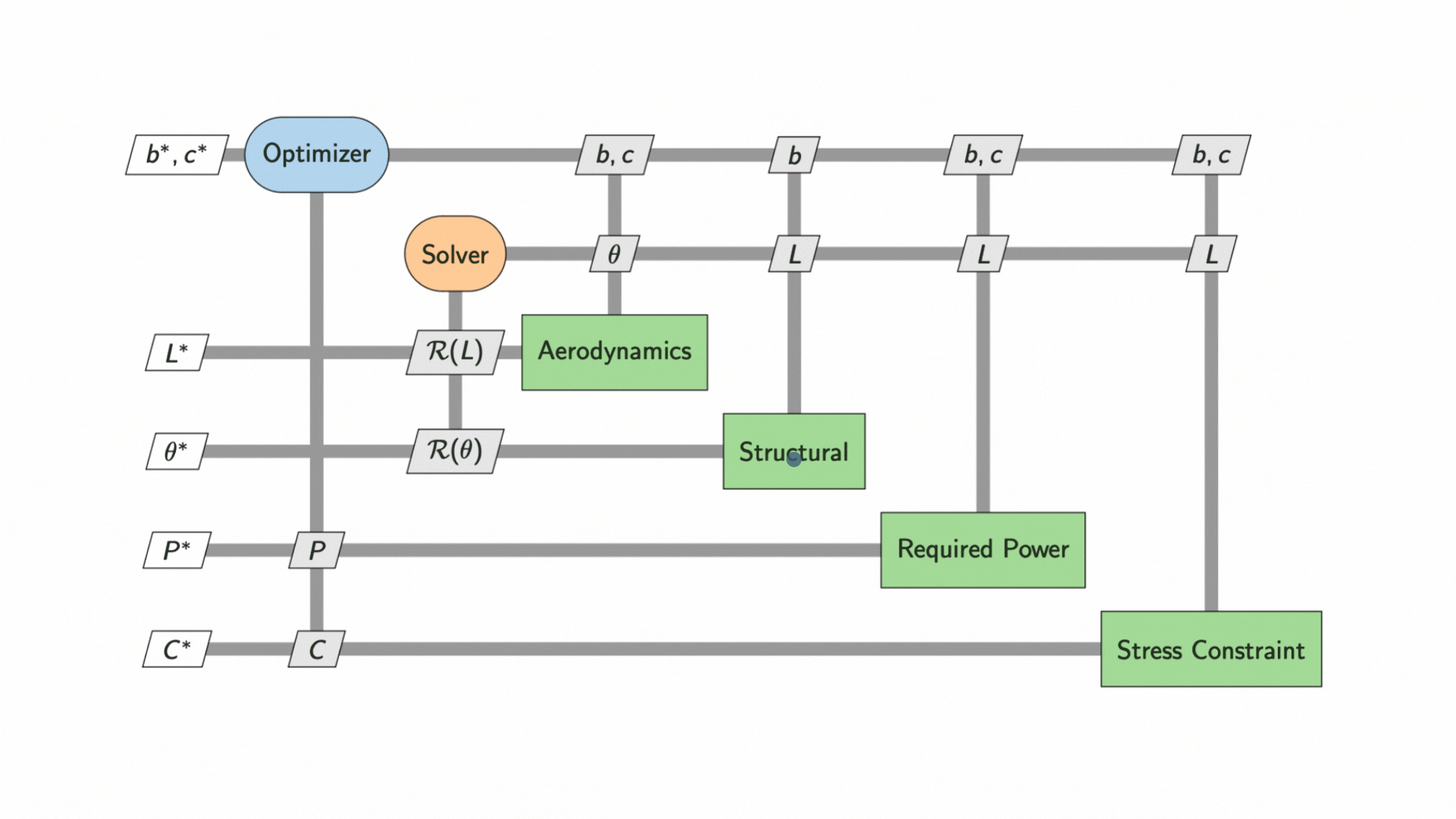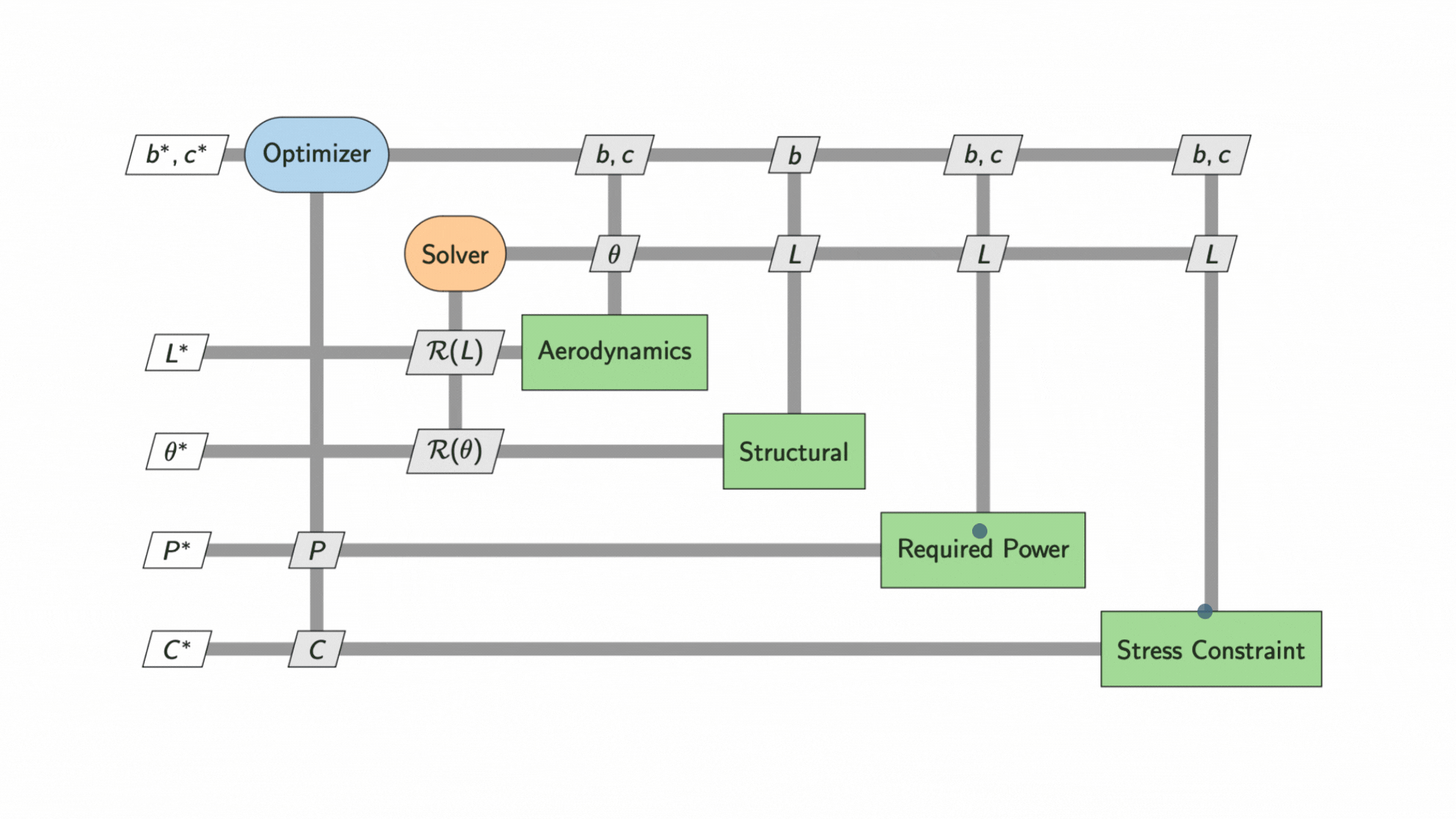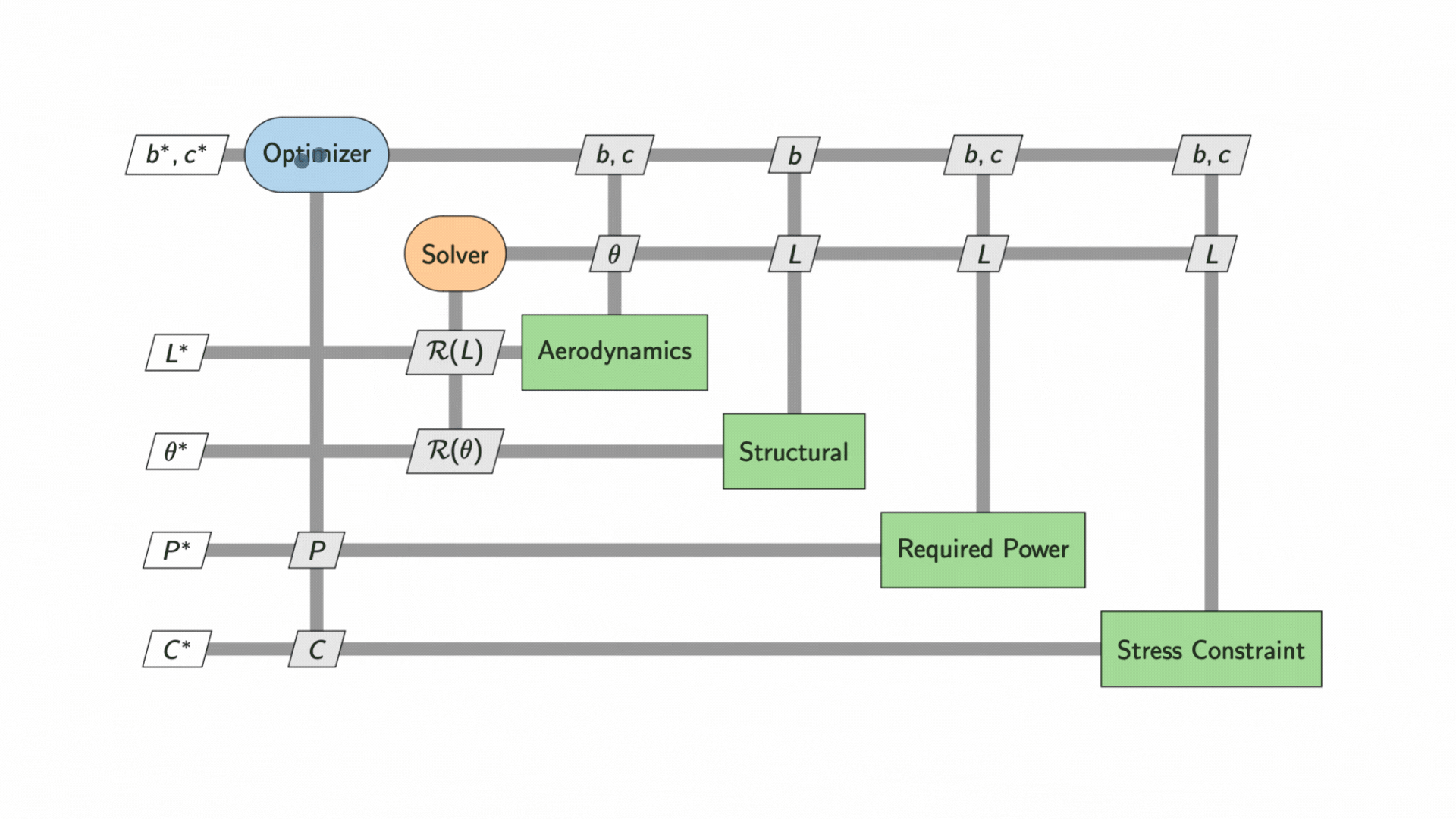
An optimizer then updates the values of ![]() and
and ![]() , iterating the process to produce an ideally lower
, iterating the process to produce an ideally lower ![]() . Gradient-based optimizers are generally more efficient than gradient-free optimizers because they have information on the best descent direction in the design space. However, they are more costly to set up as they require calculating partial derivatives, either analytically or computationally.
. Gradient-based optimizers are generally more efficient than gradient-free optimizers because they have information on the best descent direction in the design space. However, they are more costly to set up as they require calculating partial derivatives, either analytically or computationally.
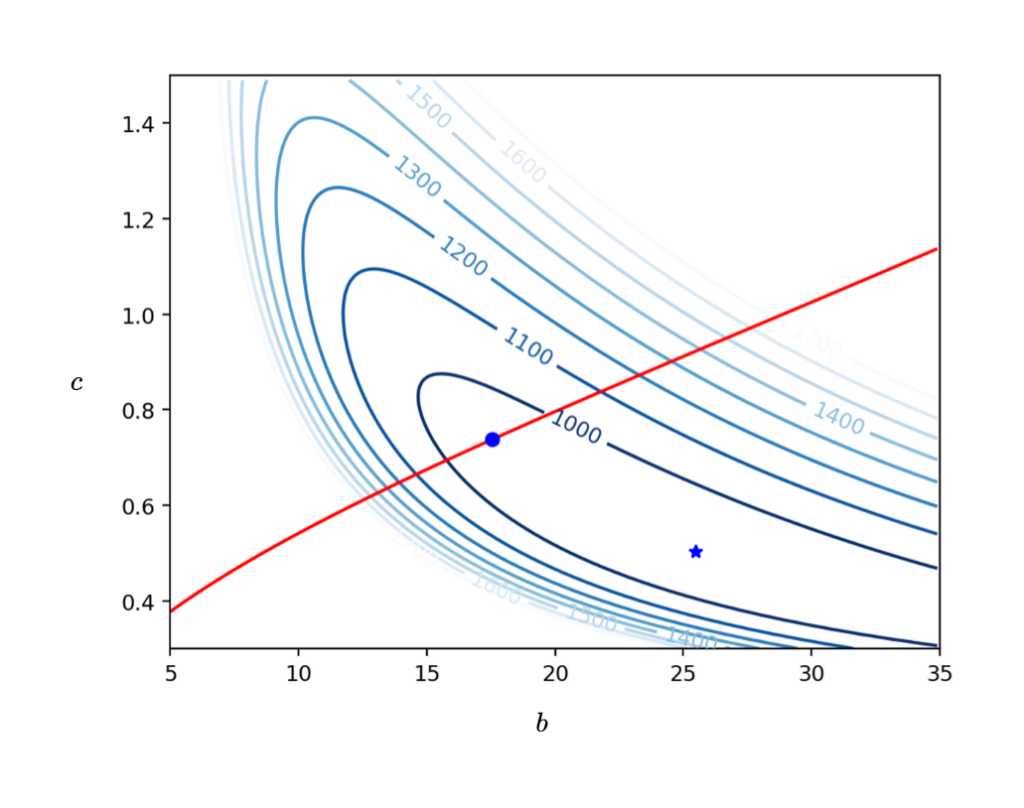
The process continues until the optimal values for wingspan, ![]() , and chord,
, and chord, ![]() are found. The plot below shows the contours of required power,
are found. The plot below shows the contours of required power, ![]() , against the design variables. The unconstrained optimal design point (star) results in a wing that has a long wingspan and a short chord. With the stress constraint (red line) in place, the optimal point is shifted towards a more realistic aspect ratio.
, against the design variables. The unconstrained optimal design point (star) results in a wing that has a long wingspan and a short chord. With the stress constraint (red line) in place, the optimal point is shifted towards a more realistic aspect ratio.
** Lift is given by the lift equation — ![]() , where
, where ![]() ,
, ![]() ,
, ![]() are density of air, wing surface area, lift coefficient respectively. Lift coefficient,
are density of air, wing surface area, lift coefficient respectively. Lift coefficient, ![]() , is a function of wing deflection,
, is a function of wing deflection, ![]() .
.
Using a simple beam bending theory and an assumption of uniform lift distribution, the wing deflection, ![]() , is given by
, is given by ![]() , where
, where ![]() is the Young’s modulus and
is the Young’s modulus and ![]() is the second moment of inertia of the wing section. This shows that the deflection angle,
is the second moment of inertia of the wing section. This shows that the deflection angle, ![]() , is dependent on lift,
, is dependent on lift, ![]() .
.
MDO for Business
A remarkable example2 of large-scale MDO applied to the design of a small satellite showed that an 80% improvement can be achieved in data download performance. Yet, despite its potential, Multidisciplinary Design Optimization remains primarily an academic pursuit rather than a common practice in the industry. High overhead and steep learning curve are the major barriers. Organisations that prioritise pragmatism often settle for “good enough” designs derived from sequential optimization. As a result, opportunities are missed and the full potential of their designs remain untapped.
To overcome these hurdles, OptimiSE offers targeted solutions to implement our proven methodology and workflow. Using MBSE principles, we develop system models that orchestrate MDO across different disciplines within the system. This can integrate with trade studies, business intelligence, or other automated tools. Once set up, teams can focus on more revolutionary and innovative design work, while MDO meticulously refines it to its optimal version.
Book your free initial consultation today to explore our tailored solutions for your needs.
In this article, we’ve peeked into the workings of MDO. Unlike sequential optimization dominant in the industry, MDO finds the true optimum, producing superior products. Employing MDO can significantly enhance collaboration between diverse design teams and elevate system development.
There are many other use cases for MDO beyond the aerostructural example. Perhaps your industry can benefit from MDO too. Feel free to leave a comment below and let us know!
¹ Lambe, A.B. and Martins, J.R.R.A. (2012). Extensions to the design structure matrix for the description of multidisciplinary design, analysis, and optimization processes. Structural and Multidisciplinary Optimization, 46(2), pp.273–284. doi:https://doi.org/10.1007/s00158-012-0763-y.
² Hwang, J.T., Dae Young Lee, Cutler, J. and Martins, J.R.R.A. (2014). Large-Scale Multidisciplinary Optimization of a Small Satellite’s Design and Operation. Journal of Spacecraft and Rockets, 51(5), pp.1648–1663. doi:https://doi.org/10.2514/1.a32751.

Leave a Reply